Dynamic spectrum allocation is becoming more prevalent in practice,
requiring frequency-agile transmitters with amplifiers capable of
high-efficiency operation at multiple operating frequencies and power
levels based on system needs and limitations. This focus session paper
presents a simplex algorithm that is expected to be useful in the
real-time fast reconfiguration of power amplifier circuits for wireless
communications and radar as they reconfigure between frequencies.
Circuit optimization algorithms originally intended for
computer-aided design (CAD) applications can be used for real-time
optimization.
Bandler, Charalambous, and Steer describe multiple algorithms useful
for generic CAD circuit optimization, including simplex (used in this
paper), pattern, and gradient searches [1] [2] [3]. In real-time reconfigurable amplifiers, adaptive amplifier output matching networks are needed. Tunable matching networks using micro-electrical mechanical systems (MEMS) devices are discussed by Lu and Vaka-Heikkila [4], [5]. Real-time impedance matching is discussed by Deve and Sun [6] [7] [8] [9]. Qiao demonstrates a reconfigurable low-power communication amplifier using a genetic tuning algorithm [10], and Baylis, Martin, and Fellows demonstrate unconstrained and constrained optimizations using a gradient-based approach [11] [12] [13].
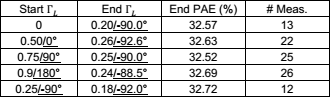
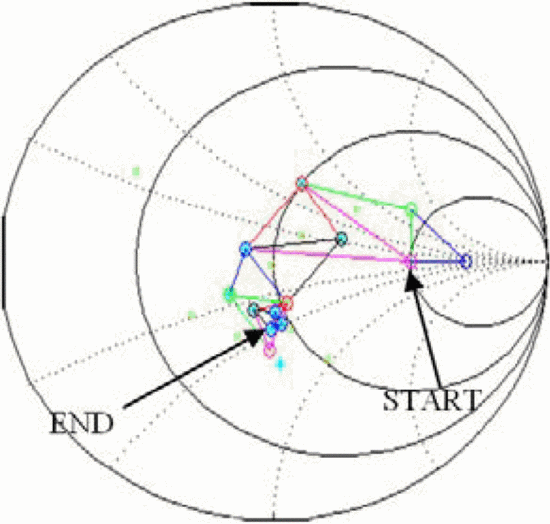
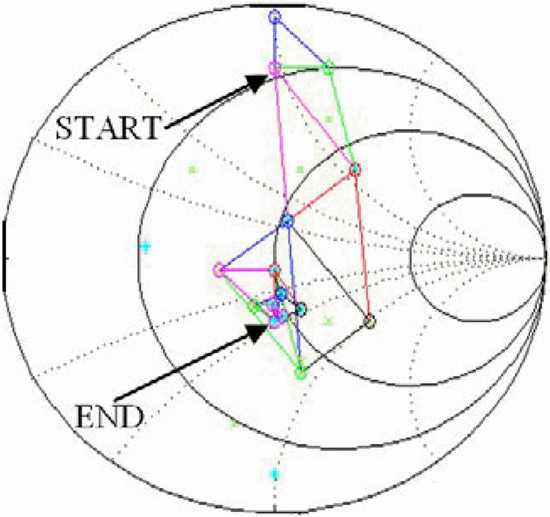
This paper demonstrates the use of simplex in amplifier load-impedance
optimizations. To our knowledge, this paper represents the first direct
application of simplex optimization to optimize in the load-reflection
coefficient 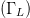 $(\Gamma_{L})$ plane.
$(\Gamma_{L})$ plane.
SECTION II
SIMPLEX CIRCUIT OPTIMIZATION APPROACH
The simplex method originally presented by Nelder and Mead [14] and discussed by Bandler [1]
has been applied to our work presented in this paper. In our algorithm,
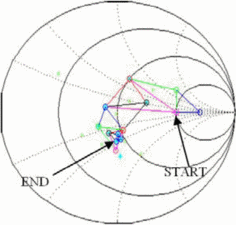
the search is performed in the Smith Chart, which is the complex plane
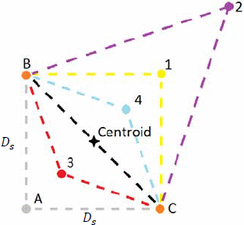
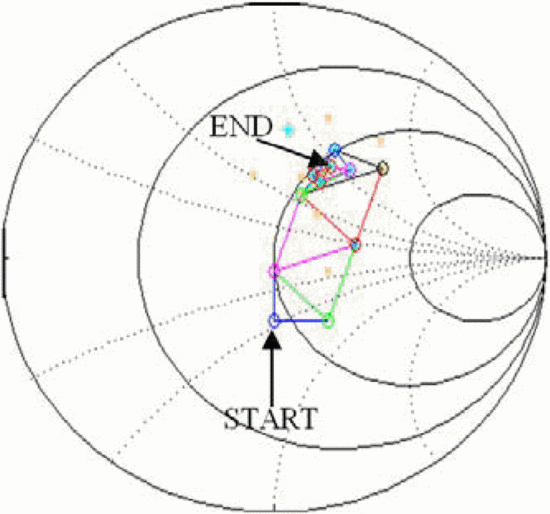
of the load reflection coefficient 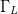 $\Gamma_{L}$. Figure 1
shows how the search unfolds. The first point of the simplex is
established at the designated starting point, shown as point A. An
additional point is then measured in each coordinate direction of the
search space, separated from the initial point by
$\Gamma_{L}$. Figure 1
shows how the search unfolds. The first point of the simplex is
established at the designated starting point, shown as point A. An
additional point is then measured in each coordinate direction of the
search space, separated from the initial point by 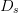 $D_{s}$
(points B and C). The “simplex” is the polygon connecting each of the
evaluation points. In two dimensions, the initial simplex is a right
triangle.
$D_{s}$
(points B and C). The “simplex” is the polygon connecting each of the
evaluation points. In two dimensions, the initial simplex is a right
triangle.
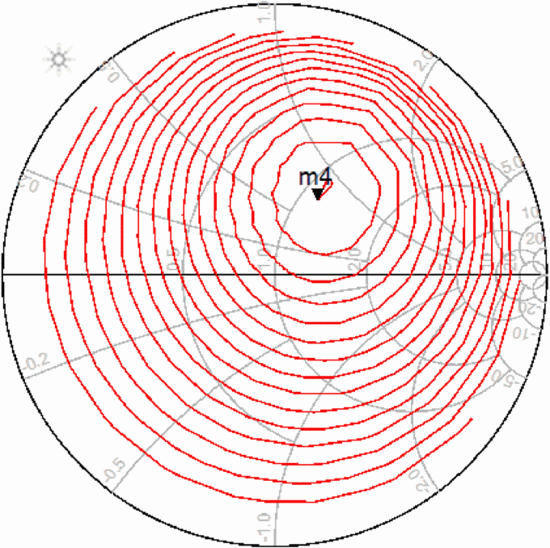
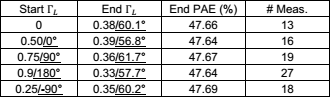
Power-added efficiency (PAE) is used as the optimization criterion
for maximization, and is first evaluated at each point of the initial
simplex (points A, B, and C). The value of 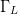 $\Gamma_{L}$ in the simplex possessing the lowest PAE (the worst value of the criterion) is then replaced by a new point [1].
$\Gamma_{L}$ in the simplex possessing the lowest PAE (the worst value of the criterion) is then replaced by a new point [1].
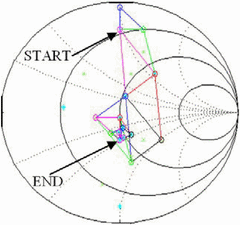
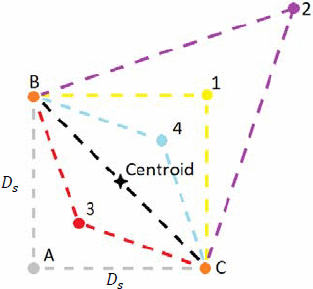
Figure 1 also illustrates how the replacement
simplex point is selected in the case where point A has the lowest
(worst) PAE of the original simplex. In this
case, PAE is next measured at point 1, the reflection of point A about
the centroid of the line connecting the two remaining simplex points B
and C [1]. If point 1 has a greater (better) PAE value than both B and C, an additional point is measured at a factor 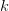 $k$
times the initial distance from the line between the other two points
(point 2). The PAE at point 2 is then compared with the PAE at point 1.
If the PAE at point 2 is greater than the PAE at point 1, then the next
simplex consists of points B, C, and 2. This is known as expansion
of the simplex. If the PAE at point 2 is lower than at point 1, but
point 1 has higher PAE than both B and C, the simplex operations resume
using the simplex consisting of points B, C, and 1. If the PAE at point 1
is greater than at point A, but less than the PAE at both B and C, then
the new simplex consists of points B, C, and 4 (point 4 is
$k$
times the initial distance from the line between the other two points
(point 2). The PAE at point 2 is then compared with the PAE at point 1.
If the PAE at point 2 is greater than the PAE at point 1, then the next
simplex consists of points B, C, and 2. This is known as expansion
of the simplex. If the PAE at point 2 is lower than at point 1, but
point 1 has higher PAE than both B and C, the simplex operations resume
using the simplex consisting of points B, C, and 1. If the PAE at point 1
is greater than at point A, but less than the PAE at both B and C, then
the new simplex consists of points B, C, and 4 (point 4 is 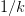 $1/k$
times the distance between the centroid and point 1). If point 1 has
lower (worse) PAE than the original worst simplex point A, the new
simplex point is placed on the original side of the mirroring line at a
distance
$1/k$
times the distance between the centroid and point 1). If point 1 has
lower (worse) PAE than the original worst simplex point A, the new
simplex point is placed on the original side of the mirroring line at a
distance 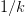 $1/k$ between this line and the original worst point A (this is point 3 in Fig. 2).
Simplex operations are re-performed using the simplex consisting of
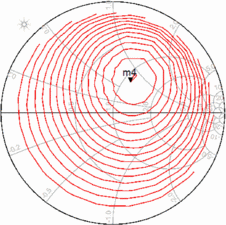
points B, C, and 3. The search ends when the distance from the centroid
to the new simplex point falls below a prespecified resolution distance
$1/k$ between this line and the original worst point A (this is point 3 in Fig. 2).
Simplex operations are re-performed using the simplex consisting of
points B, C, and 3. The search ends when the distance from the centroid
to the new simplex point falls below a prespecified resolution distance 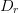 $D_{r}$. The highest-PAE point of the final simplex is chosen as the optimum.
$D_{r}$. The highest-PAE point of the final simplex is chosen as the optimum.
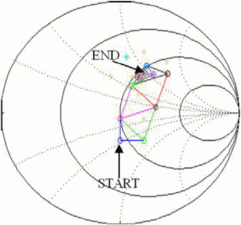
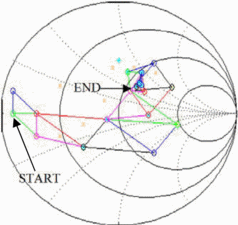
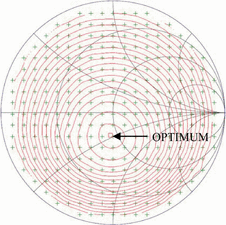
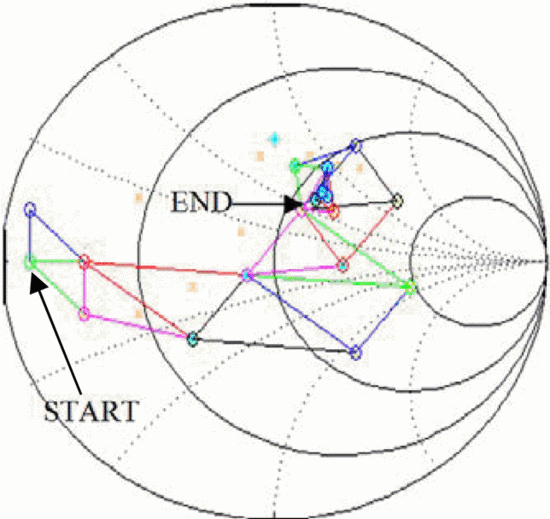
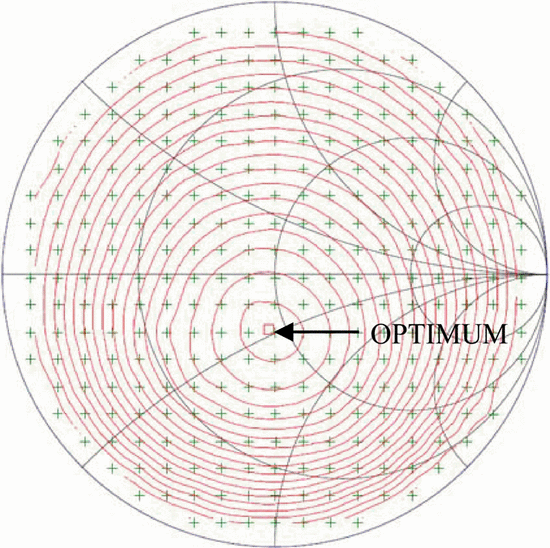
A simplex algorithm for fast load-pull search in the Smith Chart has
demonstrated in simulation and measurement. The algorithm has been
designed for intended application in a fast, reconfigurable amplifier
for use in a frequency-agile transmitter. Ongoing work that cannot be
included in this paper due to space limitations, includes constrained
optimization, which allows the optimum PAE meeting adjacent-channel
power ratio requirements to be quickly found. In addition, ongoing work
shows that the simplex method performs very well in comparison to
gradient and pattern load-pull searches.
Acknowldegments
This work has been funded by the National Science Foundation (Grant
Number ECCS-1343316). The authors wish to thank Lawrence Cohen of the
Naval Research Laboratory for helpful collaboration in this work. In
addition, the authors gratefully acknowledge the support of Keysight
Technologies in providing cost-free loan of the Advanced Design System
software, and Modelithics for donation of simulation model libraries
through the Modelithics University Program.